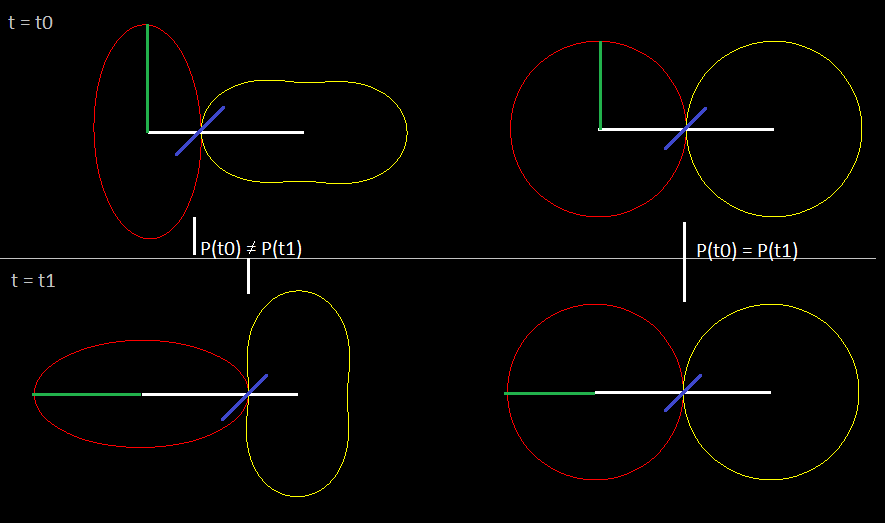
"Now, to build involute tooth profiles from this action we need to pick some way to determine tooth phase, and a pressure line."
Wow. This is essentially what I had in mind, only I was of the opinion that "picking" my own pressure line and tooth phase would not constitute something I could advertise as legitimate involute teeth, but rather my own personal bastardization of a precisely defined concept. :D I have not had time to extensively review and understand in-volute tooth theory to know how much is good enough (I am involved in too many projects... )
This discussion is very motivating to me! If we can come up with a feasible definition I can definitely implement it in Gearify! :)
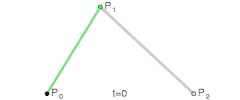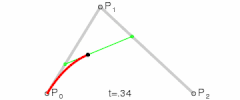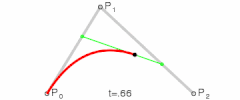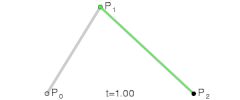
Here is my question for you though, Nate. By whatever definition you're working with, what is the pressure angle measured from on a non-circular gear? In circular gears, the line tangent to the roll lines at the point of contact is always perpendicular to the line through the centers of rotation (which gives us some nice properties). On non-circular gears (especially the more eccentric ones) the tangent line can be quite far from perpendicular to the line through the center. See the diagram below:
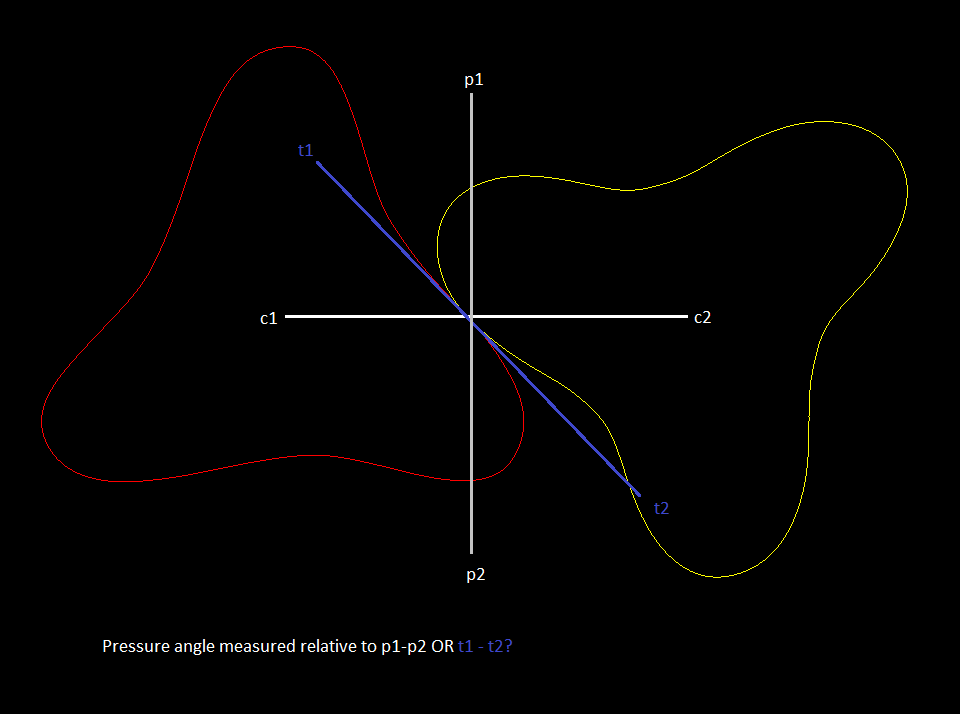
If measured from (p1-p2) I feel that there would be severe disortions where t1-t2 differs significantly. But if from t1-t2, the gears may not "push" on eachother properly and the entire benefit of involute teeth is compromised.
Thoughts?