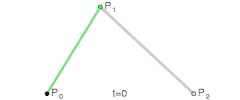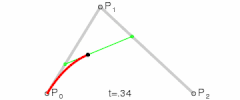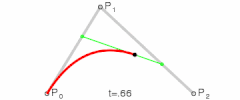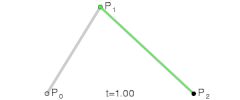
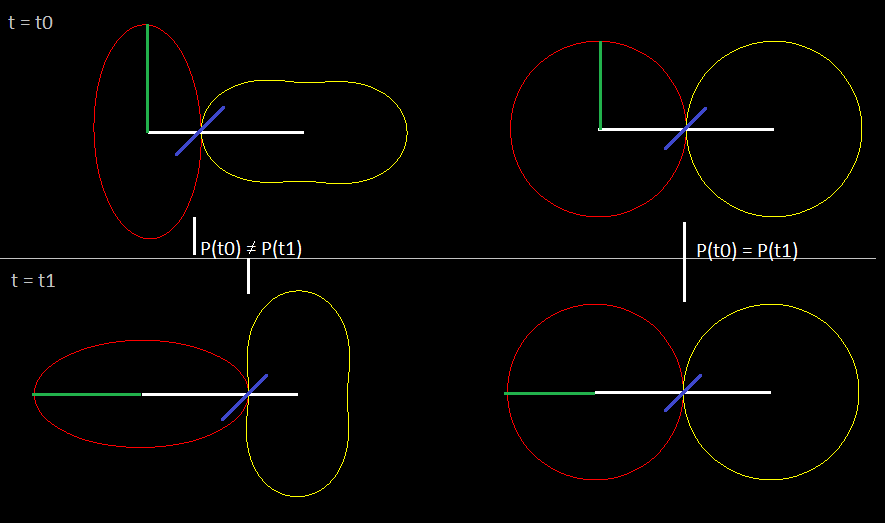
I don't know what the official definition is or even if there is one for non-circular gears. Art and I discussed the same question in the other thread. As far as I'm concerned, the preferred usage is the angle off p1-p2.Gearify wrote: Here is my question for you though, Nate. By whatever definition you're working with, what is the pressure angle measured from on a non-circular gear? In circular gears, the line tangent to the roll lines at the point of contact is always perpendicular to the line through the centers of rotation (which gives us some nice properties). On non-circular gears (especially the more eccentric ones) the tangent line can be quite far from perpendicular to the line through the center.
Mechanically speaking you probably want to measure the angle from p1-p2 and live with the distortions. That's what I was trying to describe, and, mechanically, you want the action to be close to that line. There's a lot of freedom in tooth profiles, so the roll line tangent line can somtimes also work.If measured from (p1-p2) I feel that there would be severe disortions where t1-t2 differs significantly. But if from t1-t2, the gears may not "push" on eachother properly and the entire benefit of involute teeth is compromised.
Thoughts?
In the illustration, if we imagine that we're turning the red gear clockwise as the master and the yellow gear is the slave and the gear flanks are roughly perpendicular to the t1-t2 line, then it's likely that the gears would just separate.